True Audio Checker - Algorithm Details
CD Authenticity Detector (Aucdtect)
Aucdtect (CD authenticity detector) algorithm has been developed to help determine the authenticity of musical CDs. By evaluating the character of audio data a CD contains, Aucdtect can distinguish between original studio-based recordings and those that have been "reconstructed" using a lossy audio source, such as MP3.
Aucdtect Algorithm Details
The mathematical algorithm analyzes the Fourier-spectra of the signal-time segments throughout a recording, and makes calculations of the character-bound frequency, and phase, on every time segment. The ultimate determination of recording source is made through the analysis of the spectral statistical properties. The testing protocol employs the use of both modern and antique recordings of a varying quality levels. Aucdtect's algorithm has proved to be extremely accurate in its analyses and its conclusions on recordings' origins.
It is no secret that the Internet and file-sharing networks are literally overloaded with music. Lossy formats-like MP3-offer the highest degree of compression, and are easily the most popular means of file-sharing. When played through relatively low-fidelity audio systems, the sound offered by such files is often indistinguishable from CD quality audio-to the average human ear. However, lossy-encoded audio tracks fare poorly when played on Hi-Fi systems, or when enjoyed through a pair of quality stereo headphones.
Since the untrained ear is an unreliable detector, the purchase of traditional audio CDs has given rise to a new concern-the authenticity of the audio data they contain. Here is a sample collection of audio CDs, purchased between 2000 and 2004 in Russian stores. As you can see, approximately 25% turned out to be so-called "fake" audio CDs, produced from lossy audio sources-most likely from low quality MP3s.
The suggested algorithm for addressing the question of a recording's authenticity is the following:
1. On each time segment of data the logarithm of the spectral power [2] with small additive constant is calculated. A small constant ε is used to exclude the logarithm calculation error:
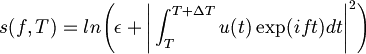 (1)
(1)2. A scatter of the logarithm of the spectrum values is calculated. The maximum frequency on which scatter sharply increases is considered to be a bound one, that corresponds to a maximum character frequency in the audio signal spectrum not connected with numerical or statistical noise σ [3].
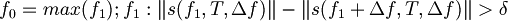 (2)
(2),where || s(f,T,Δf) || is scatter of the s(f,T) values in the frequency interval [f,f + Δf].
3. Based on the statistical distribution of the bound frequencies the set of character frequencies are determined - average bound frequency and most probable bound frequency.
4. Phase characteristics of the signal spectra are statistically processed to obtain the phase distribution of the high-band part of the signal.
5. Aucdtect's algorithm uses the calculated signal characteristics as input for a specially created and learned (by the genetic algorithm technique) original neural network with multilevel processing, and uses results from this network output to statistically conclude whether of not the artifacts exist (by Bayes-like algorithms).
6. The conclusion for the whole audio disk can be made by the maximum likelihood method (providing the most accurate solution) using neural network outputs for all audio tracks and statistical distributions, obtained in algorithm learning mode.
Our testing has demonstrated the stability of the Aucdtect algorithm in recognizing as authentic both modern and older recordings, spanning genres from classical to pop music. Predefined discs of lossy encoding reconstruction have shown an equally stable record of accuracy and reliability.
References
- R.E.Blahut, Fast algorithms for Digital Signal Processing, (1985), 446.
- G.A.Korn, T.M.Korn, Mathematical handbook for scientists and engineers (1968) 832.

